Predicting Future Nodes in Houdini & Nuke
March 10, 2025 · 7 min read
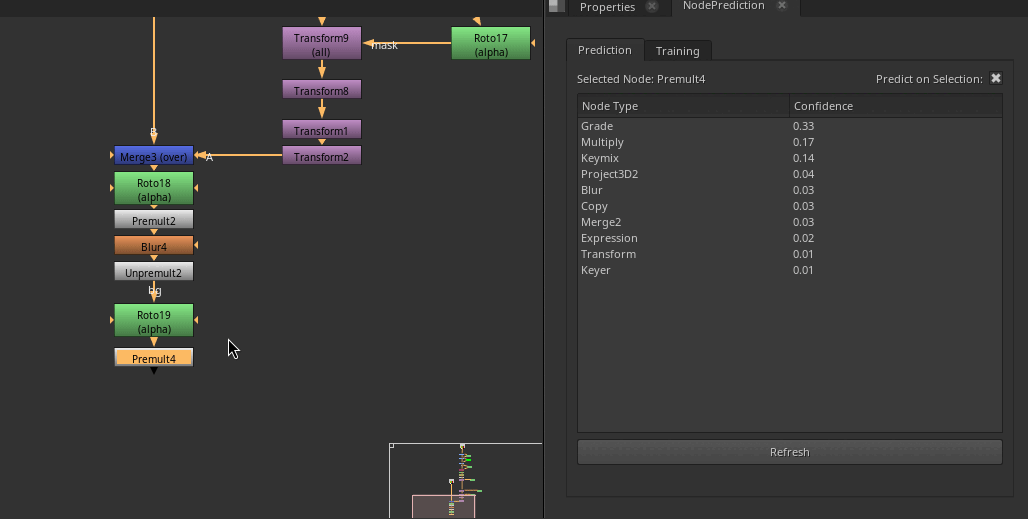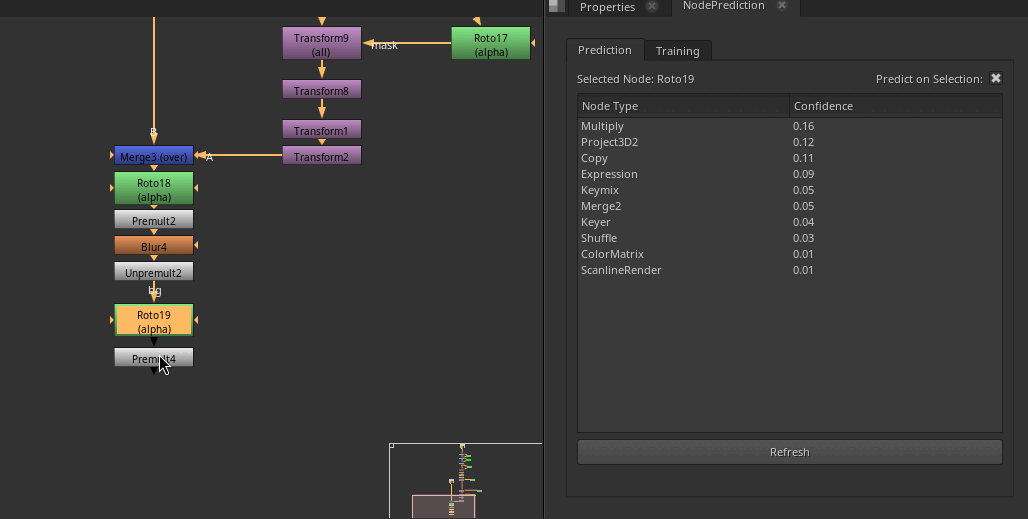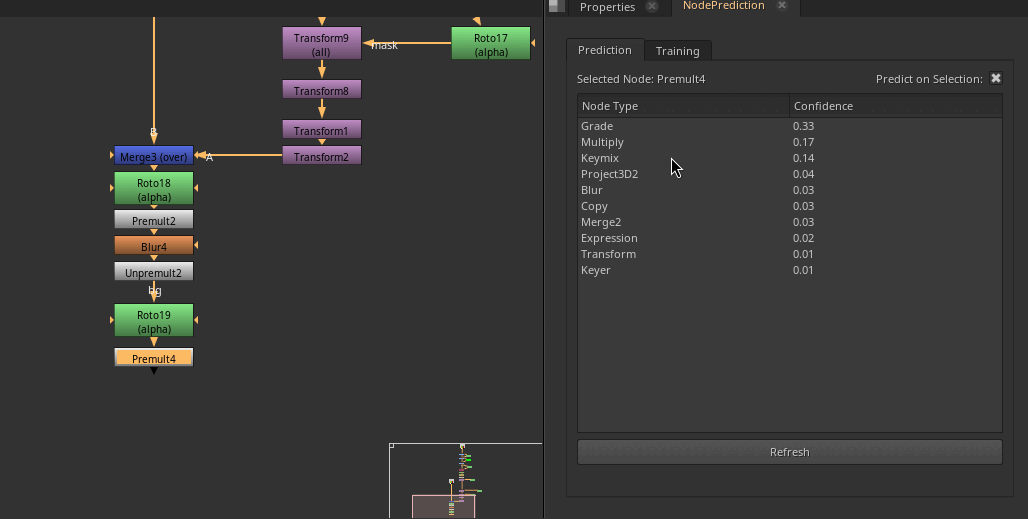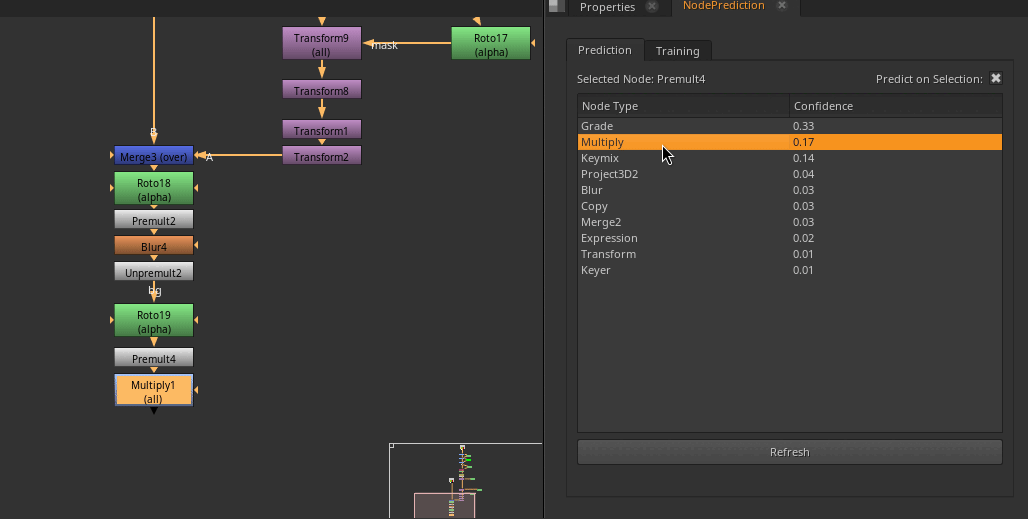
Example of the Node Prediction in action!
Overview
Inspired by Paul Ambrosiussen's Tensorflow experiment with node prediction in Houdini, I experimented with training graph-based machine-learning models to predict future nodes in applications like Nuke and Houdini. The question was straightforward: could we train a model on existing scripts to suggest useful next nodes in a workflow?
The answer? It works... somewhat. If anything the cognitive overhead of reviewing node suggestions would probably slow down workflows. The practical applications of graph-based machine learning might be more relevant for asset relationship management, automating QC processes, or attempting to standardize common workflows.
To better understand how these models work, I've attempted to document my learnings below:
Introduction to Graphs
To start, a graph represents the relationships (edges) between a collection of entities (nodes).
VFX applications like Nuke and Houdini base their workflows around node-graphs, where operators (nodes) transform data and pass it along connections (edges) to downstream operators.
An artist might take an image, apply a blur, adjust its color, and composite it with another element—each step represented by a node in the graph.
These applications use a special type of graph: Directed Acyclic Graphs.
- Directed: These graphs specify a direction on node connections (data flows from one node to another).
- Acyclic: No cycles or loops exist (you can't feed node A into node B, then back into node A!)
Each node possesses unique properties and settings called parameters (vertex/node embeddings). These define both the node's type and its specific configuration values.
When an experienced artist works with these node-graphs, they take into account any upstream nodes, their unique transformations, and the relationships between those nodes, to decide the next node to create in the graph. This is the "language" of node-based software that graph neural networks set out to learn.
Graph Neural Networks (GNN)
GNN's key feature is a concept called "message passing", essentially information sharing between connected nodes in a graph. Based on the information received from their neighbors, nodes can iteratively update their own internal representation.
The message passing process follows four key steps:
- Initialization: Each node begins with a feature vector representing its attributes (in our case, the node type and parameters).
- Aggregation: Nodes gather information from their connected neighbors, combining these signals to understand their context within the graph.
- Different GNN architectures distinguish themselves primarily through their unique aggregation methods—some use simple sums or averages, while others employ attention mechanisms to weigh neighbor importance.
- Update: Using both its current state and the aggregated neighbor information, each node transforms its representation through learned neural networks.
- Iteration: These steps repeat for several rounds, allowing information to propagate across multiple "hops" in the graph and enabling nodes to capture increasingly distant relationships.
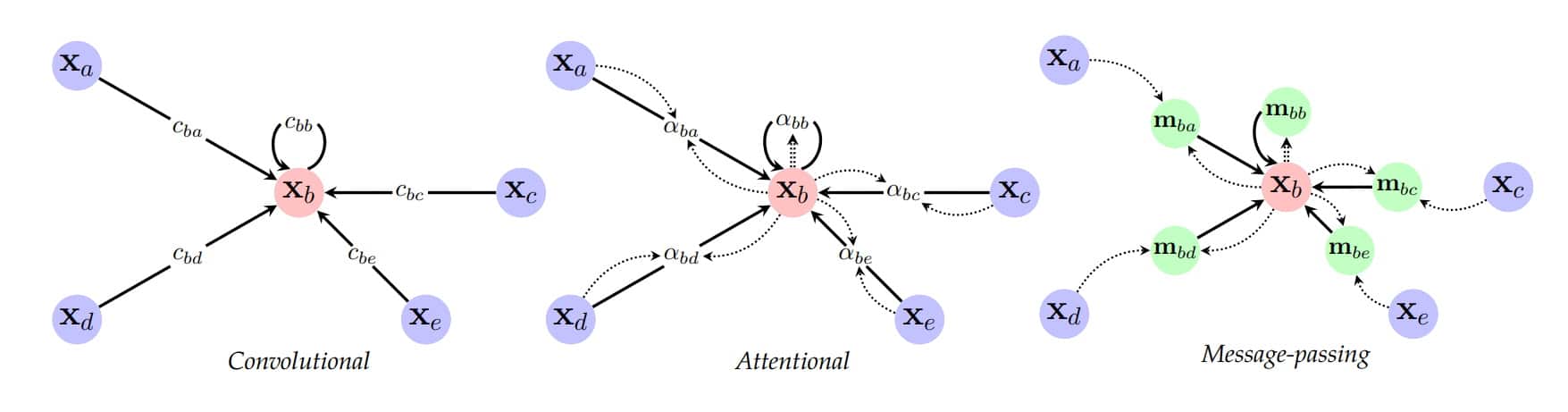
Example of Message Passing
After several iterations of passing these messages around, each node in the graph is "enriched" with information about not just itself, but any nodes in its neighborhood! With this enriched representation, we can then proceed to calculating probabilities for different node types that might come next.
Generating Good Training Examples
For the node prediction tool, I leveraged PyTorch Geometric (PyG), a specialized library for graph neural networks that extends PyTorch.
In PyG, each graph example is encapsulated in a torch_geometric.data.Data object with these essential components:
When building the node prediction tool, I relied heavily on PyTorch Geometric (PyG), an extension of PyTorch
designed to write and train graph neural networks. In PyG, each graph example is encapsulated in a
torch_geometric.data.Data object with the following components:
x: A tensor of shape[num_nodes, num_features]containing node feature vectorsnum_nodes: Each row represents one node in the graph.num_features: Each column represents a feature attribute of the node (think parameter values, etc.)
edge_index: A tensor of shape[2, num_edges]defining graph connectivity- Always contains 2 rows.
- Row 0: Source Node Indices, Row 1: Target Node Indices
- An edge from node 3 to 5 would be represented as [3, 5] in one column.
y: The ground-truth label (node type to predict)- In this example, it's a single value representing the target node type index.
edge_attr: Optional tensor of shape[num_edges, num_edge_features]for edge properties
To initialize one of these Data objects, the following steps were required:
- Script Parsing: Extract the complete node graph from Nuke or Houdini files, preserving node types, parameters, and connections.
- Example Generation: For each node in the graph:
- Designate this node as the "target" (
y) to predict - Extract all upstream nodes (ensuring some minimum number for sufficient context)
- Designate this node as the "target" (
- Feature Engineering: For each node, create a feature vector containing:
- Node Type (saved as an index in a "vocabulary")
- Parameters or other relevant values for the node.
- Connectivity Mapping: Construct the
edge_indextensor by:- Creating directed edges between all connected nodes
- Preserving input order with the
edge_attrtensor (tracking which input slot is used) - Ensuring all connections point from source to destination
Model Architecture
While there's quite a few popular graph-based architectures, I landed on a Graph Attention Network.
- Use a learnable attention mechanism which allows a node to decide which neighbor nodes are most important.
- This allows the model to pick and choose which upstream nodes might be most important when aggregating information.
A basic overview of the architecture:
- Feature Encoder: A two-layer MLP that transforms raw node features into a richer hidden representation, with LayerNorm and dropout for regularization. - These higher-dimensional latent representations allow the GNN to more effectively distribute information and capture conplex patterns.
- Message Passing Layers: Multiple GAT layers that process the graph structure, where each layer:
- Uses the GATv2Conv operator (an improved version of GAT with more expressive attention)
- Maintains connections to the initial node features through residual connections.
- Prediction Head: A three-layer MLP that processes the graph-level representation to output classification logits for possible next node types.
The model follows the general pattern of:
- Encoding information into a latent space.
- Iteratively refining that information with "message passing".
- Decoding the processed information into logits for prediction.
Issues:
- Oversquashing: As the number of layers increases, information from evaluating successively distant neighbors gets "squashed" into the same fixed-dimensional vector. Increasing the vector dimension to accommodate more data has been shown to greatly improve the performance of GAT's. [1]
- Feature Dilution: In traditional GATs, original node features can be overwhelmed by aggregated neighborhood information after multiple layers. By maintaining a weighted residual connection to the initial features throughout all layers, the model preserves important node-specific information.
...
[1] Zhou, J., Du, Y., Zhang, R., & Zhang, R. (2023). Adaptive Depth Graph Attention Networks. arXiv:2301.06265 [cs.LG]
Integration with Houdini/Nuke
Integrating ML-based tools into Houdini and Nuke presents unique challenges, as these DCCs manage their own tightly controlled environments that often conflict with dependencies required by most ML frameworks.
To overcome this issue, it seems like a simple client-server architecture might be most pragmatic. For this experiment, I used the following setup:
- A FastAPI server launched in a separate process, responsible for model inference.
- Server operates in its own virtual environment containing PyTorch Geometric and other dependencies.
- The plugin communicates with the server via basic HTTP requests.
The workflow then becomes relatively straightforward. The plugin queries the scene for the node graph structure, serializes it to JSON, sends it to the server for model inference, and then displays the resulting prediction in the application.
Resources for Further Learning
For those interested in exploring GNNs further:
PyTorch Geometric Documentation - Comprehensive library for graph-based deep learning.
Graph Neural Networks: A Review of Methods and Applications - Survey paper on GNN variants.
Adaptive Depth Graph Attention Networks - Research on improving GAT performance.
The Foundry's ML-Server - Framework for integrating ML with Nuke.